( Mathematical software used: GeoGebra )
Friday, December 23, 2011
Friday, December 9, 2011
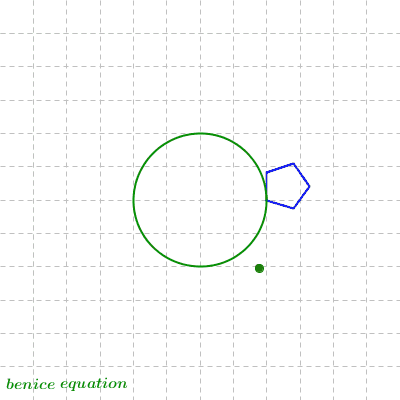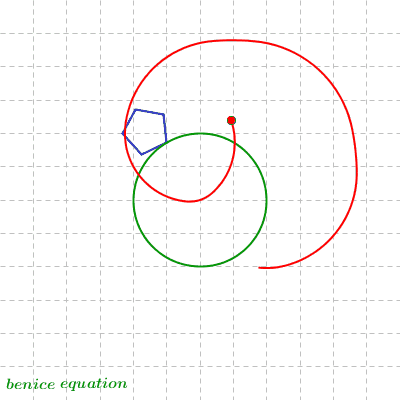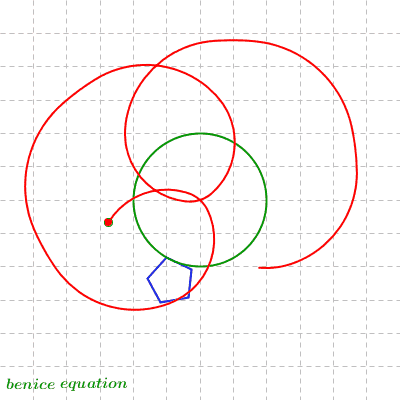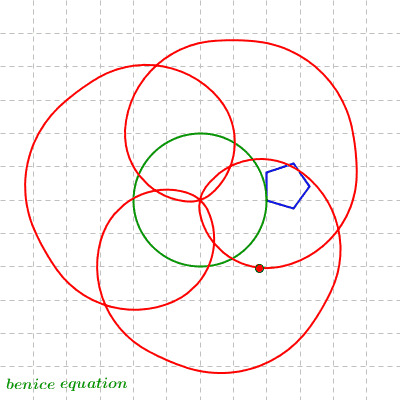
Dynamic Spirograph: Circle Rolling around Rolling Circle (1)
Circle 1 rolls around inside of the fixed base circle.
Circle 2 rolls around inside of circle 1.
( Mathematical software used: GeoGebra )
Related posts:
Wednesday, November 23, 2011
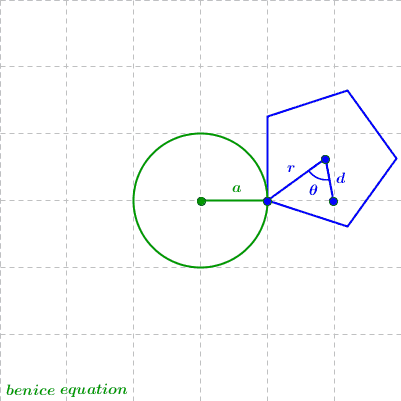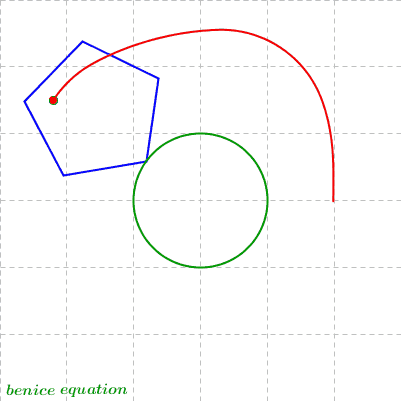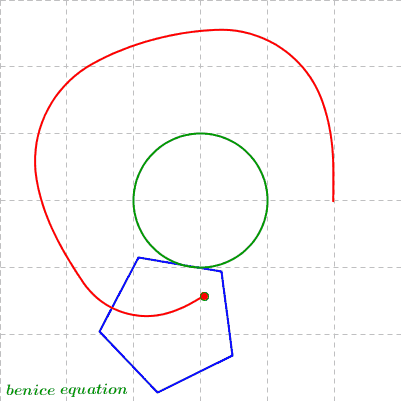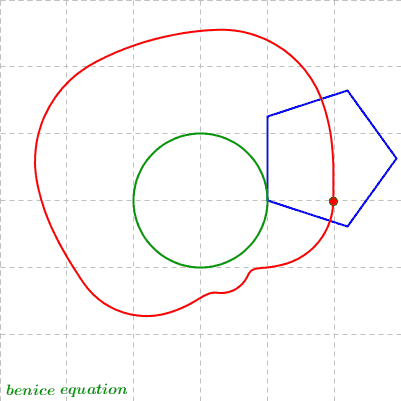
Rolling Regular Polygons around a Circle - (2) Polygonal Epitrochoid
(n = 3, k = 5/2, d = 0)
(n = 3, k = 5/2, θ = 0.5α, d = b)
(n = 3, k = 5/2, P lies on the border of the polygon.)
(The distance from P to the nearest vertex is 1/8 side length.)
(n = 3, k = 5/2, θ = 0.5α, d = 0.5b)
(n = 3, k = 5/2, θ = 0, d = 0.5r)
(n = 3, k = 5/2, θ = 0, d = 1.5r)
(n = 4, k = 4/3, θ = 0.25α, d = 0.5r)
(n = 4, k = 5/2, θ = 0.5α, d = 0.5b)
(n = 4, k = 5/2, θ = 0.5α, d = b + 0.7455a)
(n = 4, k = 11/2, θ = 0, d = 0.5r)
(n = 5, k = 3, θ = 0, d = r + a)
(n = 5, k = 3, θ = 0.5α, d = b + a)
(n = 6, k = 3/2, θ = 0.5α, d = 0.5b)
(n = 7, k = 4/3, θ = α/3, d = 0.5b)
(n = 8, k = 4/3, θ = α/3, d = 0.5b)
(n = 4, k = 8/7, θ = 0.5α, d = 0.5b)
(n = 3, k = 8/7, θ = 0.5α, d = 0.5b)
(n = 3, k = 8/7, d = 0)
(n = 3, k = 12/5, θ = 0, d = 0 ~ r)
(n = 3, k = 12/5, θ = 0, d = 0 ~ r + a)
(n = 5, k = 6/5, θ = 0.5α, d = 0 ~ b + a)
(n = 3, k = 12/5, θ = 0 ~ α, d = r)
(n = 3, k = 12/5, θ = 0 ~ α, P lies on the border of the polygon.)
(n = 2.5, 3.5, 4.5, ..., 32.5, k = 21/20, θ = 0.5α, d = b)
( Mathematical software used: GeoGebra )
Related posts:
Saturday, November 19, 2011
Rolling Regular Polygons around a Circle - (1) Polygonal Epicycloid
(n = 5, k = 3)
(n = 3, k = 5/2)
(n = 6, k = 3/2)
(n = 4, k = 1/2)
n = the number of sides of the rolling polygon
a = the radius of the base circle
r = the circumradius of the polygon
(n = 3, k = 12/5)
( Mathematical software used: GeoGebra )
Related posts:
Subscribe to:
Posts (Atom)