Rolling Regular Polygons around a Circle - (2) Polygonal Epitrochoid

(n = 3, k = 5/2, d = 0)

(n = 3, k = 5/2, θ = 0.5α, d = b)

(n = 3, k = 5/2, P lies on the border of the polygon.)

(The distance from P to the nearest vertex is 1/8 side length.)

(n = 3, k = 5/2, θ = 0.5α, d = 0.5b)

(n = 3, k = 5/2, θ = 0, d = 0.5r)

(n = 3, k = 5/2, θ = 0, d = 1.5r)

(n = 4, k = 4/3, θ = 0.25α, d = 0.5r)

(n = 4, k = 5/2, θ = 0.5α, d = 0.5b)

(n = 4, k = 5/2, θ = 0.5α, d = b + 0.7455a)

(n = 4, k = 11/2, θ = 0, d = 0.5r)

(n = 5, k = 3, θ = 0, d = r + a)

(n = 5, k = 3, θ = 0.5α, d = b + a)

(n = 6, k = 3/2, θ = 0.5α, d = 0.5b)

(n = 7, k = 4/3, θ = α/3, d = 0.5b)

(n = 8, k = 4/3, θ = α/3, d = 0.5b)

(n = 4, k = 8/7, θ = 0.5α, d = 0.5b)

(n = 3, k = 8/7, θ = 0.5α, d = 0.5b)

(n = 3, k = 8/7, d = 0)

(n = 3, k = 12/5, θ = 0, d = 0 ~ r)

(n = 3, k = 12/5, θ = 0, d = 0 ~ r + a)

(n = 5, k = 6/5, θ = 0.5α, d = 0 ~ b + a)

(n = 3, k = 12/5, θ = 0 ~ α, d = r)

(n = 3, k = 12/5, θ = 0 ~ α, P lies on the border of the polygon.)

(n = 2.5, 3.5, 4.5, ..., 32.5, k = 21/20, θ = 0.5α, d = b)

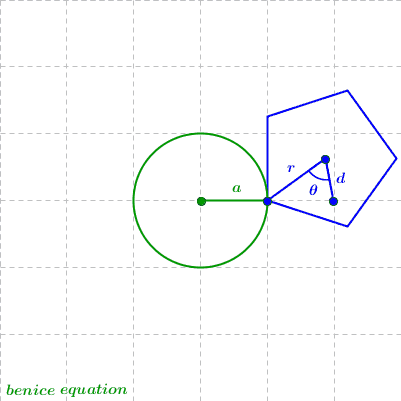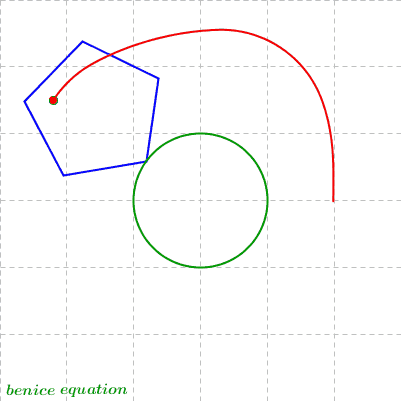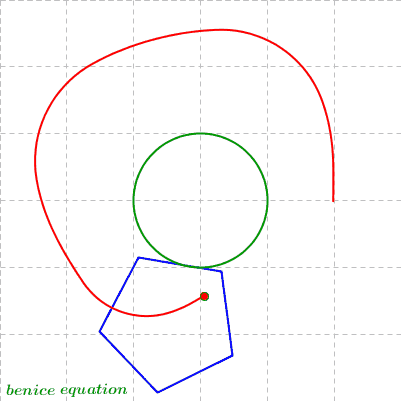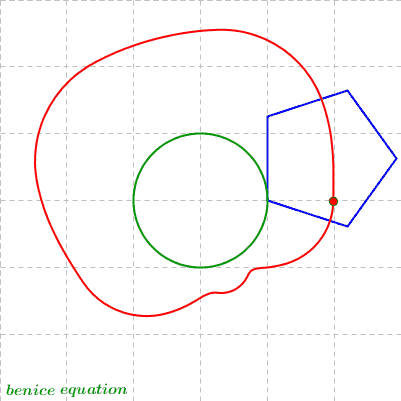
( Mathematical software used: GeoGebra )


Related posts:

• Rolling Regular Polygons around a Circle - (1) Polygonal Epicycloid