( Click on the image for a larger view. )
( Click on the image for a larger view. )
( Click on the image for a larger view. )
( Click on the image for a larger view. )
( Click on the image for a larger view. )
( Click on the image for a larger view. )
( Click on the image for a larger view. )
( Click on the image for a larger view. )
(A few images of successive zooming in on the small region are shown below.)
( Click on the image for a larger view. )
( Mathematical softwares used: GeoGebra, gnuplot )
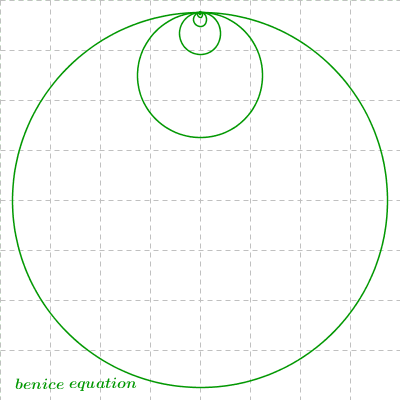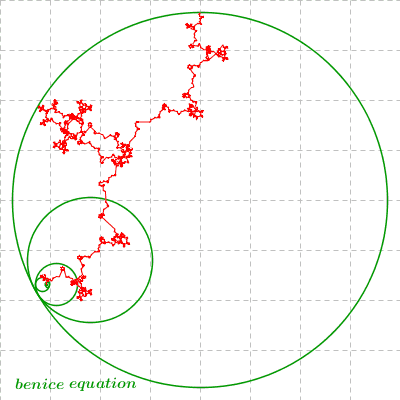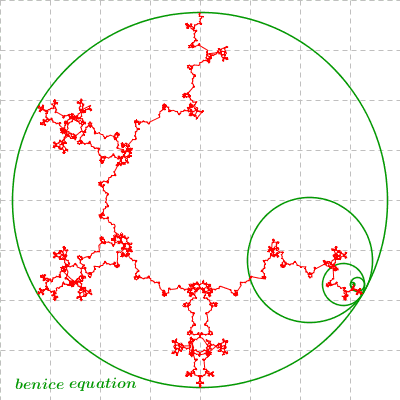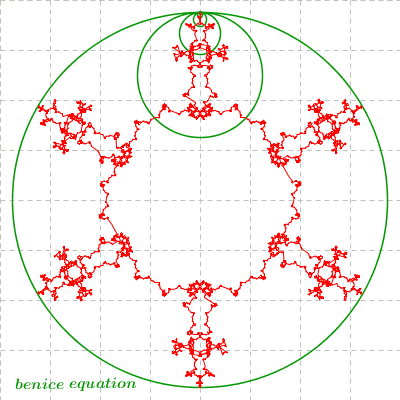
The 5th looks most like a snow-flake! Very cool.
ReplyDeleteDo you choose the speed of spinning randomly and see what will happen or you chose them for a reason? :-)
ReplyDeleteSpeed(n) = k^(n-1), k=±2, ±3, ±4, ....
Delete